Proofs and Pictures: The Role of Visualization in Mathematical and Scientific Reasoning
August 20, 2006 12:08 PM Subscribe
Proofs and Pictures: The Role of Visualization in Mathematical and Scientific Reasoning [video] "The picture is a telescope for looking into Plato's heaven." -- James Brown [cached]
yeah. Pictures can be proofs for simple cases. But induction is a general method. I would like to see someone come of with a general method of making picture proofs for complicated answers you can prove by induction.
posted by MonkeySaltedNuts at 12:38 PM on August 20, 2006
posted by MonkeySaltedNuts at 12:38 PM on August 20, 2006
Oh, fuck, that's a beautiful picture, Chuckles.
posted by orthogonality at 12:39 PM on August 20, 2006
posted by orthogonality at 12:39 PM on August 20, 2006
Yay. So... can anyone show a picture that illustrates this problem?
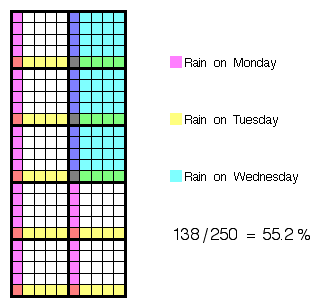
If there's a 20 percent chance of rain on Monday, a 20 percent chance on Tuesday, and a 30 percent chance on Wednesday, what's the overall chance that it'll rain during this three-day period? How do you calculate this?posted by pracowity at 12:51 PM on August 20, 2006
So... can anyone show a picture that illustrates this problem?
For n days the picture is a n-dimensonal cube. Looking at it in 2 dimensions will give you the general pictuire.
posted by MonkeySaltedNuts at 1:07 PM on August 20, 2006
For n days the picture is a n-dimensonal cube. Looking at it in 2 dimensions will give you the general pictuire.
posted by MonkeySaltedNuts at 1:07 PM on August 20, 2006
I was at that talk. While the guy was interesting, he wasn't much of a mathematician. The "picture proof" of the Continuum Hypothesis was the most laughable thing I've ever seen somebody try to present as serious mathematics.
posted by number9dream at 1:55 PM on August 20, 2006
posted by number9dream at 1:55 PM on August 20, 2006
More clearly, the uncolored squares give (7*16)/250=44.8%, the chance of no rain.
posted by Wolfdog at 2:07 PM on August 20, 2006
posted by Wolfdog at 2:07 PM on August 20, 2006
Nice work Wolfdog! And artistically attractive too.
Then there's the quirky probability version of things.
I like his poetry on this image:"The picture is a telescope for the mind's eye looking into Plato's heaven."
posted by nickyskye at 2:29 PM on August 20, 2006
Then there's the quirky probability version of things.
I like his poetry on this image:"The picture is a telescope for the mind's eye looking into Plato's heaven."
posted by nickyskye at 2:29 PM on August 20, 2006
I got really excited about this post when I saw a quote from James Brown (!) talking about math... until I realized it wasn't the right James Brown...
posted by OverlappingElvis at 3:11 PM on August 20, 2006
posted by OverlappingElvis at 3:11 PM on August 20, 2006
I entered this topic thinking that it was perhaps another James Brown, whom I have heard many good things about.
posted by Earl the Polliwog at 4:13 PM on August 20, 2006
posted by Earl the Polliwog at 4:13 PM on August 20, 2006
(Just to be sure, the picture is constructed as if the three events are independent, which models the statement of the problem, but is probably not a realistic weather model. In the absence of any other information, if you don't like the independence assumption, you can still use a block-counting picture to show that if the given information in that problem is accurate, then there's at least a 30% chance and no more than a 70% chance of getting some rain.)
posted by Wolfdog at 4:53 PM on August 20, 2006
posted by Wolfdog at 4:53 PM on August 20, 2006
How would Wolfdog's method work for this nearly identical problem:
If there's a cos(1) chance of rain on Monday, a 1/π chance on Tuesday, and a 43.2387315 percent chance on Wednesday, what's the overall percent chance that it'll rain during this three-day period (to 7 decimal places)?posted by fleacircus at 5:13 PM on August 20, 2006
You go to the store, you buy a sheet of transcendentally ruled graph paper, and proceed as before.
posted by Wolfdog at 5:19 PM on August 20, 2006
posted by Wolfdog at 5:19 PM on August 20, 2006
That could work, though knowing the area of those squares might get a bit tricky.
posted by fleacircus at 5:27 PM on August 20, 2006
posted by fleacircus at 5:27 PM on August 20, 2006
I took a course on thought experiments last semester with James Brown.
Very interesting course.
posted by spacediver at 5:37 PM on August 20, 2006
Very interesting course.
posted by spacediver at 5:37 PM on August 20, 2006
To be a little less glib, I'm a big advocate for the use of figures to help find an argument, support an argument, or be the entire argument - I'm perfectly happy with the picture versions of 1+2+...+n = (n^2+n)/2 and 1+3+5+...+(2n-1) = n^2 as essentially complete proofs that moreover contain some insight that an induction version might be lacking.
But probably the main reason math teachers spend more time teaching induction and algebra and counting techniques and epsilons and delta, and so on, is pointed up precisely by fleacircus - the cases where you can make a beautiful, insightful picture are very special ones. They're gems when they turn up, but a lot of problems just don't have nice pictures, or the picture is so hard to get to & interpret that it's not worth the effort. His pictures for the series (1/2)+(1/4)+(1/8)+... and (1/4)+(1/16)+(1/64)+... are nice - the latter one's beautiful - and they're even important when you're first trying to get the very idea that an infinite number of regions can be contained within a finite amount of area; but if that's your only technique and I do like fleacircus and tell you "Now, do the same thing to figure out what 1+(1/π)+(1/π2)+... is", (let alone Σ_{k=2}^∞ [C(n+k-2,k)*k*(k-1)/nk] )... well, good luck.
Skill with figures is an essential part of the problem-solving toolkit; Polya didn't just throw "Can you draw a figure?" in his list for the hell of it. But if it's all you've got, you're going to be out of luck; and the special cases where you can do a figure are often exactly the same neat and tidy cases that afford the best practice with induction or other symbolic techniques when you're getting acquainted with them.
posted by Wolfdog at 5:50 PM on August 20, 2006
But probably the main reason math teachers spend more time teaching induction and algebra and counting techniques and epsilons and delta, and so on, is pointed up precisely by fleacircus - the cases where you can make a beautiful, insightful picture are very special ones. They're gems when they turn up, but a lot of problems just don't have nice pictures, or the picture is so hard to get to & interpret that it's not worth the effort. His pictures for the series (1/2)+(1/4)+(1/8)+... and (1/4)+(1/16)+(1/64)+... are nice - the latter one's beautiful - and they're even important when you're first trying to get the very idea that an infinite number of regions can be contained within a finite amount of area; but if that's your only technique and I do like fleacircus and tell you "Now, do the same thing to figure out what 1+(1/π)+(1/π2)+... is", (let alone Σ_{k=2}^∞ [C(n+k-2,k)*k*(k-1)/nk] )... well, good luck.
Skill with figures is an essential part of the problem-solving toolkit; Polya didn't just throw "Can you draw a figure?" in his list for the hell of it. But if it's all you've got, you're going to be out of luck; and the special cases where you can do a figure are often exactly the same neat and tidy cases that afford the best practice with induction or other symbolic techniques when you're getting acquainted with them.
posted by Wolfdog at 5:50 PM on August 20, 2006
I think you're overstating Brown's claim, Wolfdog. You still need a hammer, even if you only have a couple of nails.
posted by Chuckles at 6:43 PM on August 20, 2006
posted by Chuckles at 6:43 PM on August 20, 2006
What is the problem with disproving the continuum Hypothesis? It is intuitively obvious that any interval on the reals has an uncountable number of intermediate values. So, is it just very very hard to show that formally, or am I just missing something? Brown said something about no well-ordering of the reals is known - is that the problem?
posted by Chuckles at 6:49 PM on August 20, 2006
posted by Chuckles at 6:49 PM on August 20, 2006
Well, I think in his talk he overplays the "I do proofs by picture, I'm a rogue who doesn't play by THE MAN's rules" kind of angle, as if there was some sort of conspiracy against pictorial arguments. Probably just to make the talk a little more exciting, because it's more fun to do something if it seems a little illicit.
posted by Wolfdog at 6:53 PM on August 20, 2006
posted by Wolfdog at 6:53 PM on August 20, 2006
I've only just gotten to the punchline of his continuum hypothesis refutation. He definitely overstates the novelty of the style of argument - whether there are pictures of darts involved or not, it's a familiar sort of "paradox" that arises when you make agruments based on probability and you allow yourself the sort of weird sets that the axiom of choice can summon into existence. At the heart of the argument is the same sort of stuff that makes the Banach-Tarski paradox (also) tick. The wiki article is pretty concise at the top: some people do view this sort of thing as evidence that AC should not be accepted as an axiom; likewise, philosophically, you may buy Freiling's argument as real evidence that CH is not acceptable as a model of "how things really work".
If you view throwing out AC and CH as a "conservative" point of view, just be aware that you can be too conservative. By analogy, the parallel postulate in geometry - which occupies a similar indecidable position based on the commonly accepted axioms - turns out to give rise to useful models of real things whether you accept it OR one of its negations. It's not unreasonable to think that CH and (not CH) both give rise to set theories that are each correct models - for different things; we're just not subtle enough yet to understand which the problems are that should be modeled with a CH version of set theory, and which shouldn't, and why.
There's a reference for Freiling's argument in this CH page.
posted by Wolfdog at 7:48 PM on August 20, 2006
If you view throwing out AC and CH as a "conservative" point of view, just be aware that you can be too conservative. By analogy, the parallel postulate in geometry - which occupies a similar indecidable position based on the commonly accepted axioms - turns out to give rise to useful models of real things whether you accept it OR one of its negations. It's not unreasonable to think that CH and (not CH) both give rise to set theories that are each correct models - for different things; we're just not subtle enough yet to understand which the problems are that should be modeled with a CH version of set theory, and which shouldn't, and why.
There's a reference for Freiling's argument in this CH page.
posted by Wolfdog at 7:48 PM on August 20, 2006
It is intuitively obvious that any interval on the reals has an uncountable number of intermediate values...
With the usual notion of order, yes; intuitively obvious and also correct. Remember, he's talking about some exotic way of ordering the reals. And his order doesn't have to be in any way compatible the usual topology (nearness relations) of the real line.
posted by Wolfdog at 7:51 PM on August 20, 2006
With the usual notion of order, yes; intuitively obvious and also correct. Remember, he's talking about some exotic way of ordering the reals. And his order doesn't have to be in any way compatible the usual topology (nearness relations) of the real line.
posted by Wolfdog at 7:51 PM on August 20, 2006
Remember, he's talking about some exotic way of ordering the reals.
Okay. And the usual notion of ordering the reals is specifically not a well-ordering (an open interval doesn't have a well defined first element, for anyone who's curious - this fact probably should have been clear from Brown's talk, I guess). I really don't have the background, and I'm starting to exhaust my attention span for the evening..
I find the attempt to apply discrete thinking to a continuous field troubling. Is that ridiculously naive?
posted by Chuckles at 9:59 PM on August 20, 2006
Okay. And the usual notion of ordering the reals is specifically not a well-ordering (an open interval doesn't have a well defined first element, for anyone who's curious - this fact probably should have been clear from Brown's talk, I guess). I really don't have the background, and I'm starting to exhaust my attention span for the evening..
I find the attempt to apply discrete thinking to a continuous field troubling. Is that ridiculously naive?
posted by Chuckles at 9:59 PM on August 20, 2006
Dang, *gush warning*, this conversation is light years above my head but it seems so cool you guys are talking about this stuff.
posted by nickyskye at 9:59 AM on August 21, 2006
posted by nickyskye at 9:59 AM on August 21, 2006
« Older Lisää löylyä? | Maybe the Chinese just enjoy having scale models Newer »
This thread has been archived and is closed to new comments

QED MF
posted by Chuckles at 12:08 PM on August 20, 2006